Introduction

Crude oil, natural gas and water are materials that are of particular importance to oil engineers. These materials, sometimes found in solid or semi-solid form (such as paraffin, gaseous hydrates, ice, and crude oil with a high pour point) at low temperatures and pressures, are found deep in the ground and in well pillars.

In liquid form, they appear as vapor phase (gas) or liquid or mostly biphasic. Solids used in drilling, cementing and fracturing operations are also used in liquid or slurry form.

The division of reservoir and well fluids into liquid and vapor phases depends on temperature and pressure. When the temperature is constant, the state or phase of the fluid in the tank changes with pressure. In many cases, the state or phase of the fluid in the tank does not match the state or phase of the fluid during production under surface conditions. Accurate knowledge of the behavior of crude oil, natural gas and water individually or in combination - under different conditions is one of the most important goals of oil engineers.

In early 1928, special attention was paid to the relationship between gas and energy, and oil engineers considered it necessary to obtain more accurate information about the physical condition of wells and underground reservoirs. Early advances in oil recovery methods revealed that calculations based on wellhead information or surface data were often misleading. Sclater and Stephenson developed the first in-well pressure recorder and sampling device for sampling pressurized fluids in wells [1]. Interestingly, this device determines the data in the well according to the positive values of pressure, temperature, gas to oil ratios and the physical and chemical nature of the fluids. The need to measure correct intra-well pressures was considered when the first precision pressure gauge was developed by Millikan and Sidol, and the essential importance of intra-well pressures in determining the most effective recovery methods and overflow processes was shown to petroleum engineers. [2, 3]. In this way, the reservoir engineer will be able to measure the reservoir pressure, which is the most important basic data required for reservoir performance calculations.

Current flow well problems

• It is difficult to maintain a constant flow rate in this type of test well. Even if the well is stable.
• It is difficult to maintain well flow when the well has just been drilled or the well has closed and re-flowed before the test well [4-11].

Most of the test well information is obtained from pressure rise analysis. Flow test analysis depends on the fluctuations of the generated flow and the change in flow causes pressure changes that increase the analysis error. In zero flow, due to the absence of pressure-derived fluctuations, there is no problem of error. However, due to the importance of daily production, closing the well for two or three days for testing is largely impossible or very difficult, therefore equipping Wells to intelligent systems (smart wells) to record pressure, time and production flow can partially eliminate the need for experimental well operations.

Application of Derivative Diagrams in the Analysis of Experimental Well Experiments

In many cases, it has been observed that derivative diagrams show the characteristics of the test well much better than the original diagrams. Sometimes a derivative diagram can be used to identify several reservoir properties that normally require a separate curve for each of them. The accuracy of derivative diagrams (pressure-time derivative diagrams) is also higher than the original diagrams [5]. In fact, 1 derivative diagrams are also a type of model diagram.

In general, the features of the derivative diagram that make the derivative a very good tool for diagnosis are:

• All flows can be seen in a graph.
• Each stream reveals a horizontal line or a line of slope n.

Using derivative diagrams simultaneously, log∆P in log∆t and log (dp / dt) in log∆t can be compared. Dimensional time and dimensionless pressure are commonly used to derive graphs.

Review the work done

In 1988, Allen and Hearn used hybrid pattern recognition and a rule-based system to identify the reservoir model and estimate the parameter. Pressure derived data were first processed to identify the actual responses. This step involves creating a design that includes symbolic shapes such as up, down, maximum, minimum, ledge, and depression. The rule-based system then uses these existing symbols and predicts possible reservoir models. Finally, the reservoir parameters are estimated using the model flow regimes and the pressure derivative diagram. The disadvantage of this method is that it requires pressure-derived data to be smoothed before the process is performed. Also, in this method, complex rules for implementing non-ideal behaviors are defined [12].

In 1988, al-Kaabi et al. Proposed a method for developing a scientific well analysis system. Their goal was to develop a mechanism to enable non-professionals in well analysis and transient testing to act like experts in petroleum science. This method is based on the interaction of well testing analysis unit and automated comparative history unit. And the user directs the interactive process in an incremental process until a custom model is created. In this method, first the type of repository is determined and continues by internal borders, then external borders are obtained. Come on. Therefore, all possible interpretive models are listed and sources are added from the data used for the probabilistic model. This method usually reduces and minimizes the problems we encounter in understanding the interpretation of the well test and does not include the interpretation of the automated model [13].

In 1989, Stewart and Doo introduced a technique for changing the derivative diagram into a symbolic case for use in the scientific system. This method is based on a test well process whose data is obtained from the smooth part of the derived diagram. The data are separated by uniformly continuous and pre-selected parameters in an approximate narrow function. Generalized Cross-validation (GCV) is the name of the uniformity band used in this method. The results of this process are printed in a table of data points by uniform optimal points that are generally replaced by the noise function. And then the uniformly derived graphs are symbolically transformed by the first approximate diagram with linear and nonlinear segments based on pre-selected errors and effective points. The details of the symbolic figure are presented from a derivative diagram, which is in the form of a digital signal or output diagram [14].

In 1990, Al-Kaabi and Lee used artificial neural networks to apply pressure well-derived data to identify the experimental well interpretation model. In this research, pressure-derived data from different reservoir models have been used to train the neural network. The authors claim that the neural network is able to effectively identify the repository model and does not need to filter the data to generalize to the network. This work only explains the quality of the test well. The calculation of reservoir parameters has not been considered in this study [15].

In 1992, Allen and Hose identified the advantages and limitations of the two methods of symbolic shapes and artificial neural networks, and aimed to combine the two different methods. To understand the model and estimate the parameters, reasoning abilities must be as good as visual abilities. They succeeded in using the neural network method for visual cognition and the symbolic shape method for reasoning abilities. In this method, which is a combination of two different methods, they intend to use neural networks to determine the design of the derivative before applying the law-based method to estimate the model and parameters [16, 17].

In 1992, Remy revised the normal course of the practical well analysis method to obtain the following results: [18]

1) Often a straight line can be found on the Herner diagram from which the necessary parameters for generating the argumentative data that should be present in the simulation can be easily obtained. However, in some cases, it is necessary. to take regression from all data and perform a measurement of the quality of analysis by selecting an appropriate model and the possible limitations.

2) Pressure-derived graphs are a type of graph that are used to identify events and are also more sensitive and permissible than logarithmic and semi-logarithmic graphs of pressure.

3) The type and method of calculations used in this work is as follows:

• Analysis of pressure and type of derivative diagrams and separation and adjustment of required data
• Find the straight line of Herner diagrams for nonlinear regression of input parameters
• Determining the reliability limits and simulating the tests with the final parameters obtained from n
• Determining the reliability limits and simulating the tests with the final parameters obtained from nonlinear regression
• Compare terrestrial data with data obtained by simulating models in dimensionless coordinates
• If the comparison is not good, choose the next model in a more complex way and repeat the previous steps

In 1993, Judyardi and Arshaghi investigated the problems of using neural networks in the analysis of wells in failing reservoirs. To solve these problems, they used the expert system, which includes two types of information, independent field data and tables including the frequency of occurrence of unrelated models. In this study, the Monte Carlo simulation method was used to provide the required statistical information for the expert system [19].

In 1993, Arshaghi, Lee, and Hasabi implemented multiple neural networks, each of which provided one reservoir model (to overcome the inefficiency of training large numbers of reservoir models). This method completely improved the presentation of each tank model. However, the calculation of reservoir parameters has not been considered [20]. In 1993, Anraco and Hern proposed a new method that distinguishes between different reservoir models using the sequential prediction probability method. This method calculated the correct model of the reservoir (using matching with all available models) and then calculated the probability that each adapted model predicts the corresponding stress responses. In this method, it is necessary to have reservoir models available and provide an initial guess of the reservoir parameters. [21]: Is a derivative of pressure, model identification, nonlinear regression and confidence intervals. The advantages of this method are as follows:

• The speed of variables can be analyzed
• More complex models can be used for analysis
• By adapting the data to the changes, this analysis can improve the response in the flow regime with data of inappropriate conditions in conventional analysis.
• Confidence intervals allow us to make a small judgment and also help us to reject incorrect answers and identify appropriate answers [22].

In 1995, Atichanagum and Hearn used an artificial neural network to identify key components of a pressure-derived diagram of several reservoir candidate models. Unit slope, ridge, fixed slope, depression, descending slope are considered as key components. In this way, the reservoir flow regime is determined and then the relevant characteristic parameters are determined using conventional methods. These parameters are then used as initial guesses for the sequential prediction probability method. The sequential prediction probability method is able to determine the best reservoir model and related unknown parameters [23].

In 1995, Cumuloy, Deltben, and Archer proposed a method that made it possible to identify a specific well test model in reasonable and consistent conditions. This reduced many of the problems associated with the process. This method is based on the application of the highest order of neural network. By using these neural networks, the same properties of the patterns can be encoded in a network architecture style. As a result, networks are able to detect test well models much more powerfully and automatically, and these networks are much faster in the law of training and training speed for the network than other conventional neural networks. They act [24].

In 1995, Song et al. Used a neural network to identify an interpretive well model. In this study, they selected the Reversed Disseminated Neural Network (BP) with the Hough Transform (HT) technique to overcome the problem and used a single neural network instead of a series of networks. The Hough Transform technique has been proven to be a powerful tool in computer image recognition and virtual image technology. With the help of the Hough Transform method, any simple pattern can be extracted from a set of pressure-derived diagrams that include irrelevant points and outliers. Using the Hough Transform extraction model, they minimized the amount of data used to identify the experimental well model in the reversed diffuse neural network [25].

In 1996, Qiang used the neural network to identify the interpretive model of the well. In this research, pressure derivative diagrams, different well interpretation models, as educational examples have been used to teach the feedback diffuse network. Next, to evaluate the performance of the neural network, the regressed diffuse network was tested with simulated data, incomplete data, noisy data, and field test well data. The results show that the artificial neural network can well distinguish the interpretive model of experimental well data, incomplete data and noisy data [26].

In 1996, Sinhala introduced a new method based on a Cohen artificial neural network called Latin (SOF) Kohonen, known for its self-organizing feature. In this method, the mapping method is used to identify the interpretation of well test models, which is based on the design of well test data on a two-dimensional vector distance that provides unique maps. With the help of this method, it is possible to analyze a large amount of well test data in various reservoirs that are more effective at the same time, which is not possible using conventional methods [27].

In 1997, Cheng proposed a new method for identifying the experimental well interpretation model, using artificial neural networks and expert systems. First, artificial intelligence was used to identify the pressure derivative diagram of the test well model, and then it was adjusted by a contract recognition system with an intelligent system. Artificial neural networks have been used to identify the experimental well interpretation model. Finally, neural networks and intelligent systems have been used together to interpret experimental wells. The author claims that this method can detect incomplete or noisy test well data [28].

In 1998, May and Dougley introduced a hybrid system for well analysis. The authors claim that the designed hybrid network has significant advantages in terms of reducing training time and allowing the participation of symbolic and numerical data. In this paper, the structure of the network and its advantages and disadvantages compared to previous methods are presented [29].

In 2000, Cook and Karakaya used a neural network to identify an interpretive model of an experimental well based on a derived diagram. In this research, neural network training is performed based on a published reversal algorithm for a range of analytically generated well-test responses. The trained network is then used to identify the test well model from the test data (not used in the network training phase). Neural network simulator and generator of analytical response within one.

In this package, a distributed structural module is used, which significantly reduces the possibility of saturation of neural networks. In addition, the distributed module allows network training to begin on different computers, so it can reduce training time by up to 16 times [30].

In 2005, Jirani and Mohebbi estimated the initial stress using artificial neural network and permeability and shell coefficient using conventional methods. In this study, they trained a multilayer neural network using field test data. The data used include test well data from three conventional reservoirs and two dual porosity reservoirs. The results of neural network parameter estimation and conventional methods are compared with the results obtained from Herner diagrams. They also claim that trained neural networks can be used to generate test well data [1].

In 2005, Kharat and Razavi used neural networks to determine the reservoir model. In this study, they used pressure-derived graphs to determine the reservoir model. Fifty pressure-derived diagram data have been used by various models to train the network to identify the relevant reservoir model. In fact, each network is trained to identify a specific reservoir model. The output of the network is a number between one and zero, which indicates the probability of matching the input diagram and the corresponding reservoir model [31].

In 2007, Aljami and Artkin used an artificial neural network as a tool for transient pressure analysis in dual porosity reservoirs. In this paper, one of the proposed transient pressure double porosity models is selected to describe natural rift reservoirs. Analytical model solution is used to generate transient pressure data, which determines the characteristic parameters of dual porosity reservoirs. The transient stress responses are obtained by forward-looking analytical solution of the polynomial fitting algorithm. Therefore, the mentioned double porosity system can be represented by a polynomial, a multiple of five. These coefficients, the known properties of dual porosity reservoirs, the characteristics of reservoir fluid and well parameters, form the main inputs given to the artificial neural network that have been used to train the network. The artificial neural network is then used inversely to predict the unknown desirable properties of the dual porosity system, including slit permeability, matrix and slit porosity, and matrix permeability [32].

In 2008, Kharat and Razavi used neural networks to determine the reservoir model. In this study, they used pressure-derived graphs to determine the reservoir model. Fifty pressure-derived diagram data have been used by various models to train the network to identify the relevant reservoir model. In fact, each network is trained to identify a specific repository model. The output of the network is a number between one and zero, which indicates the probability of matching the input diagram and the corresponding reservoir model [33]. In Kharat and Razavi study, four different neural networks have been used to identify four reservoir models.

In 2011, Waferi et al. Were able to identify the oil reservoir model using advanced and backward artificial neural networks. They considered 8 different models, which were: homogeneous reservoir and dual porosity reservoir without boundaries, homogeneous reservoir and dual porosity reservoir with 3 different boundaries (single fault without flow boundary, outer boundary of constant pressure, outer boundary completely closed). Their results showed that the detection of these models was done with a very low error rate and the models were well detected. Also, based on the comparison between the forward and backward networks, they concluded that the backward network performs much better than the leading network in recognizing the model as well as the noisy data [34].

An overview of the work done on horizontal wells

In 1949, Van Euerdingen and Hurst proposed a new way to solve fluid flow problems called Laplace transform. And then they provided a useful tool for very difficult problems in the shortest time using the Fourier series. Both sets of solutions with pressure constants and final velocity constants were expanded in both finite and infinite reservoirs [35].

In 1973, Green Garten and Remy developed the ability to solve transient flow problems by discovering the use of the source function and the Newman expansion method. Much of the work done for horizontal well problems has used the Annie Green function technique to solve three-dimensional convergence penetration problems. Although the advantage of the Newman expansion method over the Green function and the origin functions has long been known, it has not been widely used because it is more difficult to extend the Green function. They proposed a table of instantaneous function and source functions that could be used by the Green expansion method for general solutions to a wide variety of reservoir flow problems. They also proposed new solutions for the unlimited source coefficient [36].

In 1985, Doyav, Muranol, and Bordarott proposed the design of a horizontal well and its interpretation methods. They developed analytical solutions using personal computers and interpreted the design well using logarithmic and semi-logarithmic analysis. And have successfully proven two types of currents that occur in a horizontal well: a vertical radial flow and a horizontal quasi-radial flow that can interpret straight half-logarithmic lines that incorporate conventional semi-logarithm analysis. They provided detailed time criteria for determining the start and end times of the course of these flows [37, 38].

In 1988, Kouchak et al. Proposed an interpretive method for measuring transient pressure in a horizontal well, and used this measurement method for a horizontal wellbore. They considered the use of pressure data only, especially for wells with constant pressure boundaries, to be a major obstacle to the determination of the measured reservoir system and its parameters. They considered two techniques: first, the importance of system components, which must be obtained from direct methods such as: logarithmic derivative diagram, semi-logarithmic diagram, logarithmic loop, and so on. The second method is a strong nonlinear estimation method that should be used to correct the previous model and also all the transient system responses are absolutely necessary to create a model and estimate its parameters for buildup and drowdown measurements [39].

In 1991, Odeh and Babu stated that four flow cycles may occur during transient behavior from a horizontal well. They also note that most users who use additional semi-finite or unlimited assumptions at the xy level will achieve transient behavior in a horizontal well, but some of the hypotheses can lead to incorrect results that have a borderline effect. It flows over these four periods. The behavior of transient current from a horizontal well requires a real physical system without change. Analyzes should be performed on a drainage volume with closed boundaries and true heterogeneity and length and position of the well. They provided build-up and drowdown measurements to describe the behavior of these four flow periods [40].

In 1991, Kouchak et al. Proposed a new real-time analytical solution in the form of a Laplace transform for horizontal wells confined to the horizontal plane boundaries at the top and bottom of the well. Two states were considered for these two boundaries: the first state was both impermeable upper and lower boundaries, the second state was the first boundary at constant pressure and the second boundary was without flow. This new solution can use build up and drowdown tests for horizontal wells with both fixed and non-constant pressure boundaries, and the Laplace extension form can be used to obtain solutions including Intra-well storage and crust impact are used. Solutions based on the same flux are different from solutions based on medium pressure. They also identify new flow regimes and simple equations and specific criteria for the period. Presented different currents that occur during the instantaneous test [41].

In 1991, Azkan and Rakhon demonstrated the advantages of using the Laplace transform technique and the power of the source function method to solve transient flow problems. They are derived from source function solutions in the Laplace transform region, and have an extensive library of well pressure and response description solutions for a wide variety of well shapes, such as vertical, horizontal, and well wells. With hydraulic failure. And they considered all these solutions for the limited and unlimited system [42].

In 1991, they described the results of considerations in well response and described the pressure for the problems presented in the first part of the new solution for testing well analysis. They proposed a new asymptotic expression to describe the pressure in the volume of the drainage package applicable during the flow period of the system. These expressions can be used for slope factors derived for a variety of complementary conditions from vertical, horizontal and vertical fracture wells. They also explored fixed speed solutions with more complex conditions [43].

In 1991, Ahaeri and Wu proposed a fast and efficient algorithm for calculating horizontal well pressure using the well-analyzed verb analysis well. Both methods have a source function method with Laplace inversion algorithm. Real distance gives accurate results for a wide variety of wells and reservoir conditions including: well constant pressure, well storage, shell coefficient and liquid phase redistribution. They also described the use of their own horizontal well algorithm solutions in interpreting build up test data [44].

In 1991, Tamang proposed several topics for the interpretation of transient pressure tests on horizontal wells including, identification of flow regimes, direction of Herner diagrams, and analysis of multiple velocity tests. Insert a line [45].

In 1993, Kamal, Boehidma, Smith, and Johns showed that the length of a horizontal well may be less than the length of a horizontal drilled and completed piece. They proved that incorrect horizontal well length or incorrect descriptive flux can lead to incorrect estimation of well and reservoir parameters from transient pressure tests. On the other hand, these errors increase kx and decrease ky and kz. Therefore, the effective horizontal well length should be estimated before the transient pressure test analysis. They developed, reviewed, and evaluated a new model called the fragmented horizontal well model. This model includes the impact of producing a horizontal well with separate sections. This model enables engineers to produce Combine with realistic data or provide any other information that suggests the possibility of flow distribution from the horizontal well, and obtain more realistic well transient pressure data and reservoir parameters [46].

In 1994, Do and Stuart stated that in horizontal well measurement analysis, the reservoir arrangement should be visualized in three dimensions. They provide a range of possible transient pressure derivative responses for horizontal wells in homogeneous reservoirs under the geometry of diverse horizontal boundaries, including: unlimited lateral boundaries, single boundary, no-flow boundary cut in half, and parallel boundaries with shapes. Different ups and downs (either or both without flow or with gas cap, blue). Analytical solution, typical derivative response, derivative diagram analysis, and derivative diagram detection for the mainstream regime. Is a person. They also provided simple equations and specific criteria for different flow periods that occur during the instantaneous test [47].

In 1995, Metr and Santo stated that there were two ways to interpret well tests at any given time [48]:

1- Piece analysis method, which is an attempt to identify and analyze unique flow regimes, for example, storage in the well, vertical radial flow, horizontal radial flow, horizontal linear flow and reservoir boundaries governing the flow.

1- The complete model method, which is supposed to describe a well and a reservoir, create a combined pressure forecast and compare the measured data.

They also outlined the advantages and limitations of these two methods, and introduced the fractional analysis method for further identification of possible models and estimation of the relevant reservoir characteristics, and then a supplementary model for calculating all flow regimes and Separation of the obtained results from fragment analysis is used.

In 2002, Mir Asaf Sultan and his colleagues used a method to identify horizontal well models using neural networks, and the identification methods they performed included: identifying and interpreting the well test model, identifying flow regimes, and locating Flow regimes are based on derivative diagrams. They considered 11 different models, two models of homogeneous reservoir and dual porosity with one boundary, and other models examined the effect of different regimes [49].

Neural Networks

Brain Structure

Every biological neuron as a community of organic matter, although as complex as a microprocessor, does not have the computational speed of a microprocessor [50-73]. Some neural structures are made at birth and others throughout life, especially early in life. They are created and consolidated. Biologists have recently discovered that the function of biological neurons, such as the storage and retention of information, lies within the neurons themselves and the communication between the neurons. In more technical terms, learning is inferred as the creation of new connections between neurons and the rearrangement of existing connections.

The brain, as a parallel-structured processing system, has 1,011 basic units called neurons, and each neuron connects to approximately 104 other neurons. The neuron is the main element of the brain and acts alone as a regional processing unit. The way neurons work is very complex and is not yet well known at the microscopic level, although its basic rules are relatively clear. Each neuron receives multiple inputs that come together in some way. If the number of active inputs of the neuron reaches a sufficient level in an instant, the neuron will also be activated and ignited, otherwise the neuron will remain inactive and quiet. An illustration of the major features of neurons is presented in Figure 1.

Figure 1. The main characteristics of a biological neuron [12]

Perioperative Respiratory Adverse Event

Most neurons are made up of three basic parts:

• The body of the cell (which contains the nucleus and other protective parts and is called the soma)
• Dendrites
• Exxon

Which constitute the last two parts of the communication elements of neurons. Neurons are divided into three categories based on the structures between which messages are conducted:

• Sensory neurons that send information from sensory organs to the brain and spinal cord.
• Stimulus neurons that carry command signals from the brain and spinal cord to muscles and glands.
• Communication neurons that connect neurons.

Mathematical model of a neuron

A neuron is the smallest unit of an artificial neural network. The body of each nerve cell consists of two parts, the first part is called the combination function, the task of the combination function is to combine all the inputs and produce a number. In the second part of the cell, there is a transfer function, which is also called the excitation function [12]. The most common types of stimulation functions are based on biological models. In fact, just as a biological cell must reach a certain stimulus threshold level to produce a signal, excitation functions produce very small output values until the combined and weighted inputs reach a certain threshold level.

Figure 2. The structure of an artificial neuron [3] when the combined inputs reach a certain threshold, the nerve cell is stimulated and produces an output signal.

When the combined inputs reach a certain threshold, the nerve cell is stimulated and produces an output signal.

Internal communication between neurons in an artificial neural network (Figure 2) is very simple. Most neural networks have one input layer, at least one hidden layer, and one output layer.

Input layer: Receives information from an external source and distributes it within the network.

The hidden layer receives information from the previous layer. Information processing is done in this layer.

The output layer receives the processed information and transmits the results to an external receiver.

Information processing within neural network neurons is done numerically. The magnitude of the signal that enters each neuron depends on two factors:

- The size of the input signal from the previous neuron.

- The weight or length of the connection between two neurons.

Network learning

1. A) Learning with the observer

In observer learning, the learning rule is that for a set of input vectors to the network and the desired network output for the inputs. After applying the input to the neural network at the network output, the output value is compared with the desired output value and then the learning error is calculated and used to adjust the network parameters, so that if the next time the same input to the network Apply the network output closer to the desired output value.

1. B) Learning without an observer

In supervisor learning or self-organized learning, neural network parameters are modified only by the system response. In other words, only the information received from the environment to the network consists of input vectors and the desired response vector is not applied to the network and the classification of input patterns and indicators in the inputs and the relationship between them is set by the network It becomes.

1. C) Intensified learning

This algorithm is a special mode of supervised learning that instead of using the desired output, uses a criterion only to determine how good the output of the neural network corresponding to an input is. An example of this type of learning algorithm is the genetic algorithm. In this type of learning, instead of providing a real answer, it is presented to the numerical network, which indicates the level of network performance.

Classification based on structure

1. A) Feed networks

In these networks, signals flow from the input layer to the output layer through one-way connections. Single-layer neurons are connected to next-layer neurons but have no connection to their layer neurons. Feeder networks establish a constant connection between the input and output space, meaning that the output at a given moment is only a function of the input at that instant. MLP, LVQ, GMDH networks are examples of feeder networks [30].

1. B) Return networks

In a recursive network, the output of some neurons is returned to the same neuron or neurons of the previous layer. As a result, the signal can flow in both directions. Return networks have a dynamic memory, meaning that their output at a given moment is a reflection of the instantaneous input and previous inputs and outputs. Hopfield, Elman and Jordan networks are among the return networks [11].

Perceptron network

Perceptron neural networks, especially multilayer perceptron’s, are among the most functional neural networks. These networks are able to perform a nonlinear mapping with desired accuracy by selecting the appropriate number of layers and neural cells, which are often not large. The learning rule of this network is of learning with the observer. In the multilayer perceptron neural network, two types of signals are generally used, which are better to be separated from each other. One type of signal moves in the direction of travel (from left to right) and the other category is signals. Which move in the return path (from right to left). The first category is called functional signals and the second category is called error signals. Figure 3 shows a three-layer MLP. Neurons in the input layer act only as spaces for distributing input signals to hidden layer neurons. Each neuron l in the hidden layer calculates the sum of the input signals multiplied by the corresponding weight and produces the output which is a function of this sum. The output of the output layer neurons is calculated in the same way.

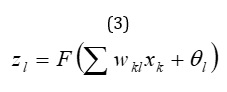
Figure 3. The structure of a three-layer MLP

Arranging data presentation to the network

There are several ways to provide training data to the network:

1- The data are entered into the network in order.

2- Data is presented to the network randomly.

3- One data is presented to the network repeatedly until the error criterion reaches an acceptable value, then the next data enters the network. Among the mentioned methods, random presentation of data to the network, the best convergence rate and reduction has an error during training. Weight correction can also be done after providing all the training data, or after providing each data, or after providing a certain amount of data to the network.

Transfer function

The function that converts the inputs of a neuron directly affects the learning process. Any function can be used to transfer the inputs of a neuron, but linear, sigmoid, and hyperbolic tangents are commonly used.

The simplest function is a linear function that transmits the inputs of one neuron to the next layer or environment without change, resulting in a range of -∞ to +∞. The linear function can be used in the input layer or the output layer, but its use in the hidden layer disrupts the learning process.

The sigmoid transfer function is often used for multilayer networks. The sigmoid function produces outputs between (1 and 0) in which the neuron inputs go from -∞ to + ∞.

In some cases, the hyperbolic tangent transfer function may also be used

End of training

Another issue with learning algorithms is when training should end. One of the following three methods can be used to do this:

1- A fixed value should be considered for the number of cycles (Epoch) of presenting all data to the network. If the results are not satisfactory at the end of the training, repeat the steps.

2- During the training, after each n round of providing data to the network, the training is temporarily stopped and the network performance is measured. Network performance can be measured against training data series or Cross Validation data series.

3- The above two methods can be combined for the training completion criterion.

Generally, the performance of a neural network is tested against a series of Cross Validation data to judge the future results of the network and also to avoid over-training of the network.

Number of neurons in the layers

The number of neurons in the input layer is equal to the number of independent parameters affecting the phenomenon under study. Also, the number of neurons in the output layer is equal to the number of variables that must be predicted. The number of neurons in the secretory layer is a variable that must be determined. Usually the value of this variable is determined based on trial and error according to the results of the network, but there are several theoretical methods to determine this variable [12]. Optimization methods such as genetic algorithms can be used to find the optimal number of neurons in the hidden layer.

Criteria for good fit

Usually, various statistical criteria are used to measure the function of the neural network, the most important of which are:

Regression analysis

Using fitting, the predicted results of the network against the desired output can be plotted in a graph called a regression analysis graph (the independent variable is plotted against the dependent variable). According to Equation (1-53), he calculated two criteria an and b, that the value of b is close to 1 and the value of a is close to zero, indicating the suitability of the function used.

Correlation coefficient

The correlation coefficient expresses the degree of correlation between the predicted results of the network and the actual data, and in other words, the covariance division of independent and dependent variables is obtained on their standard deviation. According to Equation (1-54), the correlation coefficient can be calculated. Obviously, the closer the value of this coefficient is to 1, the closer the predicted values are to the actual values.

where in:

:   Observed values (real).

 : Average values observed (real).

:   Estimated values (network output).

:   : Is the average of the estimated values (network output).

The square of the mean squares of the error

A more appropriate indicator that can be used to estimate network accuracy is the square of the mean square error. This criterion evaluates the accuracy of the model based on the difference between the actual values and the predicted values, and naturally, the closer it is to zero, the less difference there will be between them. The square of the mean squares of the error is defined by the relation (1-55).

Method of collecting test well data and neural network structure

Reservoir models intended for analysis of well test data and their detection by artificial neural network are: homogeneous, heterogeneous reservoir (dual porosity) with different boundaries including single fault with constant pressure, single fault without flow and a tank without borders, which is a total of 8 models. In the following, we will describe these reservoir models, the required parameters and the information required by the well to enter the software, and so on. The considered reservoir models are: To generate test well data, it is first necessary to know the reservoir models. In other words, the models for which the test well data is required need to be specified. In this project, eight different models that include homogeneous and dual porosity reservoirs with different boundaries have been selected for detection by neural networks.

1. Constant pressure homogeneous tank, no flow and no boundary
2. Constant pressure homogeneous tank, no flow with single boundary fault constant pressure
3. Constant pressure homogeneous tank, no flow with single fault without flow
4. Constant pressure dual porosity tank, no flow and no boundary
5. Constant pressure dual porosity tank, no flow with single fault constant pressure boundary
6. Constant pressure dual porosity tank, no flow with single fault boundary without flow
7. Double flow porosity tank without flow with single boundary fault constant pressure
8. Double porosity tank, without flow with single fault boundary without flow

Conclusion

Oil and gas masses are found inside underground traps formed by structural and stratigraphic characteristics. Fortunately, oil and gas deposits are usually in the more porous and permeable parts of the bed, which are mainly sands, sandstones, limestones, and dolomites, as well as in the intermediate interests. The grain or pore space created by the joints, cracks, and solution activity is found. In the initial state of the reservoir, the hydrocarbon fluids are single-phase or two-phase. The single-phase state may be the liquid phase in which all the gas in the oil is dissolved. In this case, dissolved natural gas reserves should be estimated as crude oil reserves. On the other hand, the single-phase state may be the gas phase. If there are evaporated hydrocarbons in the gas phase that can be recovered as natural gas liquids on the ground, this tank is called a condensate gas tank or a distillation gas tank. In this case, the available fluid reserves (condensate or distillation) should be estimated as gas reserves. When the hydrocarbon mass is two-phase, the vapor phase is called the gas cap, and the liquid phase beneath it is called the oil zone. There will be four types of hydrocarbon reserves: free gas or associated gas, dissolved gas, oil in the oilfield, and natural gas liquids recovered from the gas cap. Although the hydrocarbons in the reservoir, called storage, have constant values, the number of reserves depends on how the reservoir is operated. In 1986, the society of petroleum engineers (SPE) chose the following definition for reserves: Reserves, estimated volumes of crude oil, natural gas, natural gas liquids and associated materials available on the market from one time onwards, under the current economic conditions, with specific exploitation operations and under the current government regulations, they will be able to recover, profit and supply the market economically. Reserves are calculated using existing geological and engineering data. Gradually, as more data is obtained from the operation of the repository, stock estimates are updated.

The initial production of hydrocarbons from underground reservoirs using natural reservoir energy is the primary exploitation. In primary exploitation, oil or gas is driven to production wells by a) expansion, b) fluid displacement, c) gravity drop, and d) repulsive capillary force. If the tank has no aquifer and no fluid is injected into it, the recovery of hydrocarbon fluids is mainly by expansion of the fluid. In the case of oil, on the other hand, recovery may be by gravity. If there is an inflow of water from the aquifer or water is injected into selected wells instead, recovery is performed by a displacement mechanism that may accompany the structure. And the work of gravity or repulsive capillary force. Gas, which is a transporting fluid, is also injected into wells to help recover oil. Gas is also used to recover condensate fluids in the gas cycle. The use of a natural gas or water injection scheme is called a secondary recovery operation. When a water injection program follows a secondary recovery process, it is called a water flooding process. The main purpose of natural gas or water in the tank is to maintain pressure. For this reason, the term pressure retention program is also used to describe the secondary recovery process. Another displacement process is called the third stage recovery process. In cases where the secondary recovery processes do not work, use Finds. These processes are also used in repositories that do not use secondary recovery methods due to their low recovery potential. In this case, the word of the third stage is incorrect registration. In some repositories, it is useful to apply a secondary process or the third stage before the end of the first stage recovery process. In these reservoirs, the term extraction is used and generally includes any recovery process that improves the recovery from the reservoirs more than is expected from the natural energy of the reservoir.